Resistividade Eléctrica
Nos post anteriores abordei sobre condutores, e também disse que os metais são condutores de electricidade, mas cada metal tem suas características específicas. Por exemplo, a característica específica de bronze é diferente do ferro, assim como do ferro é diferente do estanho, e por aí em diante.
Então, se cada material metálico tem suas características especificas diferentes uma da outra, então podemos dizer que cada metal também tem uma resistividade diferente da outra.
Assim sendo, apesar de todos os metais serem condutores de electricidade, existem aqueles que são chamados, bons condutores de electricidade, como o caso de cobre ou ouro.
Conceito de Resistividade
A resistividade eléctrica de um material é a propriedade que este material tem na oposição da passagem da corrente eléctrica através de um condutor.
Vamos considerar condutores feitos do mesmo material, ou seja, com a mesma resistividade mas que diferem pelos comprimentos e pelas áreas das secções transversais, conforme indicado na figura.
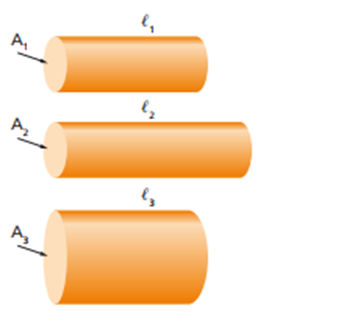
O primeiro condutor tem a mesma secção transversal maior que do segundo condutor (S1 = S2), mas o tem comprimentos diferentes, onde o comprimento do primeiro é maior que do segundo (𝓵1 < ℓ2).
Por outro lado o primeiro condutor tem o mesmo comprimento que o terceiro condutor (𝓵1 = ℓ3), mas tem diferentes áreas da secções transversais onde a área da secção transversal do primeiro é menor que do terceiro (S1 < S3).
Face aos postulados acima descritos, verifica-se experimentalmente que, tendo a mesma área da sua secção transversal (S1 = S2), apresenta maior resistência eléctrica o fio de maior comprimento (𝓵1 < ℓ2).
Nesses termos temos: ℓ2 > ℓ1 ⇒ R2 > R1. Resistência (R) directamente proporcional ao comprimento (ℓ)
Por outro lado, para condutores de mesmo comprimento (𝓵1 = ℓ3), tem maior resistência eléctrica o fio de menor área de secção transversal (S1 < S3).
Nesses termos temos: S3 > S1.⇒ R3 < R1. Resistência (R) inversamente proporcional a área (S) da secção transversal.
Em função dos condicionantes acimas é possível estabelecer uma lei segundo a qual a resistência eléctrica R de fios condutores de dado material é directamente proporcional ao seu comprimento ℓ e inversamente proporcional à sua área S de secção transversal:
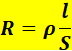
Onde:
R – Resistência eléctrica em Ohm (Ω);
ρ – Constante da resistividade eléctrica em (Ωm) ou também em (Ωmm2/m), ou ainda em (Ωcm);
ℓ – Comprimento em metros (m);
S – Área da secção transversal em (m2 ou mm2).
Quanto melhor condutor for o material do fio, tanto menor será sua resistividade. Por isso, os metais são, de um modo geral, as substâncias com menores resistividades.
Define-se a grandeza condutividade eléctrica σ do material como sendo o inverso da resistividade. Indicando a condutividade por σ (sigma), temos:
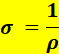
Quanto melhor condutor for o material, maior a sua condutividade eléctrica.
Tabela de Coeficientes de Resistividades
A tabela ao lado fornece, para algumas substâncias, valores da resistividade a 20 °C.
| Material | Resistividade (Ω • mm2/m) |
| Prata | 0,0159 |
| Cobre | 0,0170 |
| Alumínio | 0,0270 |
| Ferro | 0,0970 |
| Platina | 0,0980 |
| Chumbo | 0,2100 |
| Tungstênio | 0,0550 |
| Mercúrio | 0,9500 |
| Constantan | 0,49 |
| Manganina | 0,48 |
| Nicromo | 1,12 |
| Grafite | 0,4 a 0,7 |
Exemplos
1. Um condutor metálico, cilíndrico, de comprimento 50 m, possui uma área de secção transversal igual a 2,0 mm². Esse metal tem resistividade 1,6 · 10–8 Ω · m.
a) Determine a resistência eléctrica do condutor.
b) Qual é a resistência elétrica de 1,0 km desse mesmo fio?
Resolução
Antes de resolvermos vamos extrair os dados do enunciado para substituirmos na equação resolvente, mas a um dado interessante, o coeficiente da resistividade é dado em Ωm, então o valor da da área da secção devemos converter de mm2 para m2.
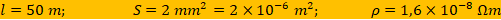
Leia sobre: Conversão de Unidades de Área.
a) Determine a resistência eléctrica do condutor.
Para resolvermos vamos usar a fórmula de cálculo de resistência, mas também será exigido que tenhas conhecimento sobre notação científica para resolver, assim fica:
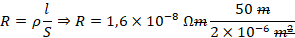
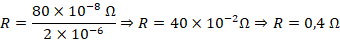
Leia sobre: Notação Científica.
b) Qual é a resistência eléctrica de 1,0 km desse mesmo fio?
Vamos antes converter o comprimento em km para metros, nesse caso para o Sistema Internacional.
1 km = 1000 m.
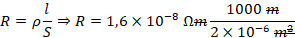
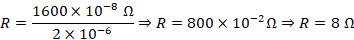
Leia sobre: Conversão de Unidades de Comprimento.
2. Um fio metálico é feito de um material cuja resistividade é 0,20 Ω • mm2/m e tem secção transversal de área 0,10 mm2. Determine a resistência eléctrica desse fio por metro de comprimento.
Como de habitual antes de resolvermos vamos extrair os dados do enunciado para substituirmos na equação resolvente, mas a um dado interessante, é que pede-se para calcular a resistência por metro de comprimento, podemos considerar comprimento igual a 1 metro.

Para resolvermos vamos usar a fórmula de cálculo de resistência, assim fica:
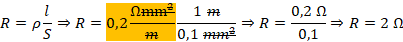


1 comentário em “Resistividade Eléctrica”