Exercícios Resolvidos sobre Oscilação Mecânica – Parte 2
4. Dados o gráfico referente ao movimento harmónico de uma partícula.
a) Determine a amplitude e o período de oscilação da partícula.
b) Calcule a frequência das oscilações.
c) Calcule a frequência angular.
d) Quantas vezes por minuto a partícula passa pela posição de equilíbrio?

Resolução
Já é sabido que o movimento harmónico é aquele que uma partícula presa numa extremidade, ela irá repetidamente realizar o mesmo movimento, com padrões e parâmetros constantes, estamos a falar da frequência e período, assim como a elongação e outros parâmetros.
Olhando atentamente o gráfico, nota-se que o tempo está dado em segundos, mas a elongação está em decímetros (dm), como os dados devem ser expressos no SI, então deve-se realizar a conversão, lembrando que 1 dm = 0,1 ou seja, 1 m = 10 dm.
a) Determine a amplitude e o período de oscilação da partícula
A amplitude é a distância máxima entre o ponto de equilíbrio, até a elongação máxima de uma das extremidades da onda (vale ou crista), note que nesse gráfico o ponto de equilíbrio é 0 dm, e a elongação máxima é +4 dm (crista) ou -4 dm (vale). Mas por se tratar de distâncias, iremos ficar com a parte positiva, logo a amplitude é A = 4 dm = 0,4 m.
Período é o tempo necessário que uma partícula leva para realizar uma volta completa. Nesse como temos de calcular o período até um certo instante, nesse caso tendo t = 26 s, devemos então contar o número de voltas que a partícula realizou, até esse instante.
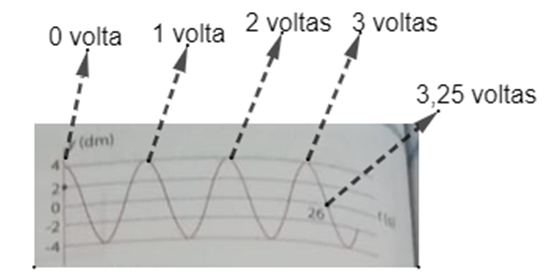
A partícula realizou ao todo 3,25 voltas, isto é, n = 3,25 voltas, dentro de 26 s, t = 26 s. Com esses dados pode-se calcular o período dessa forma:
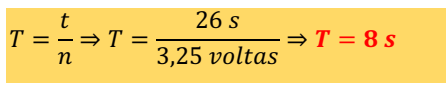
Leia Sobre: Conversão de Unidades de Comprimento.
b) Calcule a frequência das oscilações.
A frequência é o inverso do período das oscilações, dessa forma temos:
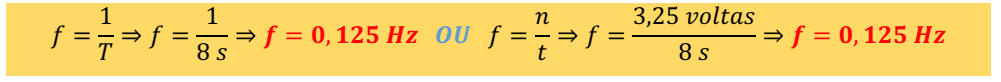
Como podes ver, o valor não alterou, então podes escolher qualquer dos métodos de resolução.
c) Calcule a frequência angular.
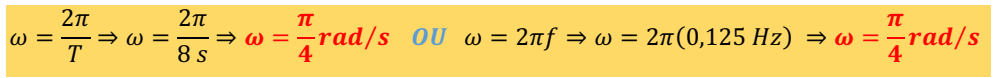
d) Quantas vezes por minuto a partícula passa pela posição de equilíbrio?
Toda partícula em movimento harmónico, passa pelo menos duas vezes pela posição de equilíbrio, na primeira na ida e a segunda na volta. Agora, pretende-se saber, quantas vezes passa da posição de equilíbrio por minuto, sabendo que 1 minuto corresponde a 60 s, assim fica:
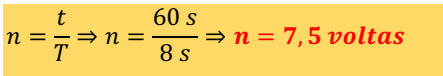
Uma vez calculado o número de oscilações, deve-se multiplicar por 2, conforme a explicação acima, ou seja, são 7,5 voltas na ida e 7,5 voltas na volta, dessa forma temos:
n = 2 ∙ 7,5 voltas
n = 15 voltas.
R: Passa pela posição de equilíbrio 15 vezes em 1 minuto.
Leia Sobre: Conversão de Unidades de Tempo
5. Os gráficos que se seguem são referentes as oscilações harmónicas de duas partículas, A e B.
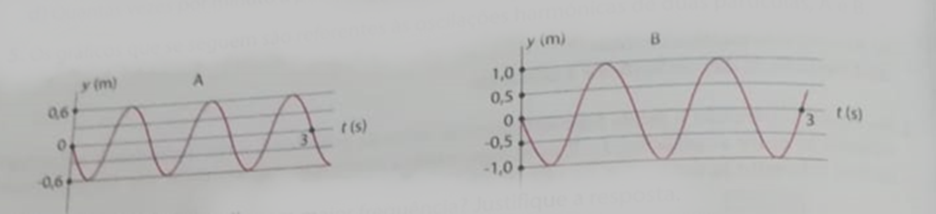
a) Qual das partículas oscila com maior frequência? Justifique a resposta.
b) Qual das partículas tem maior período de oscilação? Justifique a resposta.
c) Determine a amplitude das oscilações de cada partícula.
d) Calcule o período de oscilação de cada partícula.
Resolução
a) Qual das partículas oscila com maior frequência? Justifique a resposta.
A partícula A. Essa partícula oscila com maior frequência porque realiza mais oscilações em mesmo intervalo de tempo. Repare que em 3 s a partícula A realiza 3 oscilações, enquanto nesses mesmos 3 s a partícula B realiza 2,5 oscilações.
b) Qual das partículas tem maior período de oscilação? Justifique a resposta.
Partícula B. Se a partícula A, tem maior frequência, e sendo a frequência o inverso do período, então quer dizer que a partícula A tem menor período em comparação com a partícula B que tem menor frequência e consequentemente maior período.
c) Determine a amplitude das oscilações de cada partícula.
Partícula A
A amplitude é a distância máxima entre o ponto de equilíbrio, ate a elongação máxima de uma onda, note que nesse gráfico o ponto de equilíbrio é 0 m, e a elongação máxima é +0,6 m ou -0,6 m. Mas por se tratar de distâncias, iremos ficar com a parte positiva, logo a amplitude é A = 0,6 m.
Partícula B
A amplitude é a distância máxima entre o ponto de equilíbrio, ate a elongação máxima de uma onda, note que nesse gráfico o ponto de equilíbrio é 0 m, e a elongação máxima é +1,0 m ou -1,0 m. Mas por se tratar de distâncias, iremos ficar com a parte positiva, logo a amplitude é A = 1,0 m.
d) Calcule o período de oscilação de cada partícula.

TAMBÉM PODES GOSTAR: