Exercícios Resolvidos Sobre Equações Exponenciais: Parte 4
Resolve as equações exponenciais seguintes:
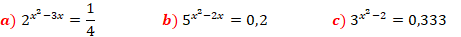
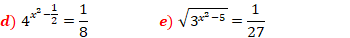
Resolução
O princípio de resolução de equações exponencias é o mesmo, onde a base do primeiro membro deve ser igual a base do segundo membro. De seguida, uma vez estando as bases iguais, eliminam-se-as, mantendo-se apenas os expoentes. Desse modo, a resolução dependerá da equação que vai resultar nos expoentes, podendo ser linear, quadrática, ou mesmo trigonométrica, etc.
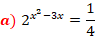
A base do primeiro membro é 2, então com isso, a base do segundo membro também deve ser 2, a fim de serem idênticos, contudo devemos passar ¼ (que é a base do segundo membro), para um valor equivalente mas com base 2, dessa forma temos:
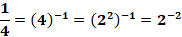
Feito isso, já temos uma potência de base 2, igual a base do primeiro membro, continuando a resolução teremos:
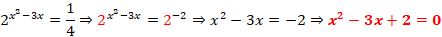
Resultou numa equação quadrática, e para encontramos os valores de x, recorremos a fórmula resolvente de uma equação quadrática, a equação x2 – 3x + 2 = 0, tem como coeficientes os seguintes valores: a = 1; b = -3 e c = 2.
Calculando o Delta temos:
∆ = b2 – 4ac
∆ = (-3)2 – 4(1)(2)
∆ = 9 – 8
∆ = 1
Calculando o valor das raízes temos:
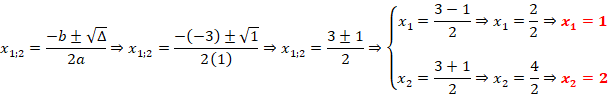
Sol = {1,2}

A base do primeiro membro é 5, então com isso, a base do segundo membro também deve ser 5, a fim de serem idênticos, contudo devemos passar 0,2 para um valor equivalente, mas com base 5, dessa forma temos:
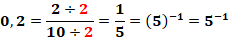
Feito isso, já temos uma potência de base 5, igual a base do primeiro membro, continuando a resolução teremos:
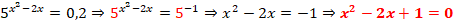
Resultou numa equação quadrática, e para encontramos os valores de x, recorremos a fórmula resolvente de uma equação quadrática, a equação x2 – 2x + 1 = 0, tem como coeficientes os seguintes valores: a = 1; b = -2 e c = 1.
Chegado nesse ponto, simplesmente calcula-se o valor de delta (∆), e depois as suas raízes (x1 e x2), dessa forma as raízes são: x1 = 1 e x2 = 1. Conforme foi feito no primeiro exercício.
Sol: {1}
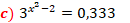
A base do primeiro membro é 3, então com isso, a base do segundo membro também deve ser 3, a fim de serem idênticos, contudo devemos passar 0,333 para um valor equivalente mas com base 2, dessa forma temos:
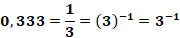
Feito isso, já temos uma potência de base 3, igual a base do primeiro membro, continuando a resolução teremos:
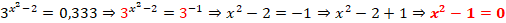
Resultou numa equação quadrática, e para encontramos os valores de x, recorremos a fórmula resolvente de uma equação quadrática, a equação x2 – 1 = 0, tem como coeficientes os seguintes valores: a = 1; b = 0 e c = -1.
Ou também pode-se optar pelo outro método, visto que a equação quadrática é do tipo ax2 + c = 0.
Os valores das suas raízes são: de x1 = -1 e x2 = 1, e como solução temos: Sol: {-1;1}
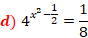
A base do primeiro membro é 4 e a base do segundo membro é 8, e matematicamente não existe um expoente que colocado em ambas as bases, irá resultar num mesmo valor, mas para tal existe uma saída, olha que tanto o 4, assim como o 8, tem 2 com o número comum, e existem sim expoentes que colocados a base 2, resultam em 4 e 8, dessa forma teremos:
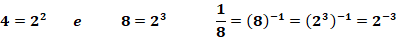
Feito isso, já temos uma potência de base 2, igual a base do primeiro membro, continuando a resolução teremos:
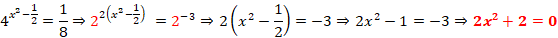
Resultou numa equação quadrática, e para encontramos os valores de x, recorremos a fórmula resolvente de uma equação quadrática, a equação 2x2 + 2 = 0, tem como coeficientes os seguintes valores: a = 2; b = 0 e c = 2.
Ou também pode-se optar pelo outro método, visto que a equação quadrática é do tipo ax2 + c = 0.
Os valores das suas raízes x1 e x2 não existem em conjunto de números reais, e como solução temos: Sol: { }
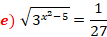
A base do primeiro membro é 3, então com isso, a base do segundo membro também deve ser 3, a fim de serem idênticos, contudo devemos passar 1/27 para um valor equivalente mas com base 3, dessa forma temos:

Feito isso, já temos uma potência de base 3, igual a base do primeiro membro, mais o primeiro membro por ter uma raiz quadrada, como forma de eliminar a raiz, ambos os membros estarão elevados a 2, continuando a resolução teremos:
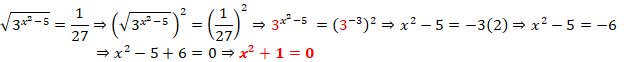
Resultou numa equação quadrática, e para encontramos os valores de x, recorremos a fórmula resolvente de uma equação quadrática, a equação x2 + 1 = 0, tem como coeficientes os seguintes valores: a = 1; b = 0 e c = 1.
Ou também pode-se optar pelo outro método, visto que a equação quadrática é do tipo ax2 + c = 0.
Os valores das suas raízes x1 e x2 não existem em conjunto de números reais, e como solução temos: Sol: { }