Exercícios Resolvidos sobre Associação de Resistências

Exercícios Resolvidos sobre Associação de Resistências: Parte 1

34. Estão associadas em série três condutores cujas resistências valem R₁ = 1 Ω, R₂ = 2 Ω e R₃ = 3 Ω. A diferença de potencial entre os extremos da associação é de 60 V.

a) Represente esquematicamente a associação e calcule a sua resistência equivalente.

b) Determine a intensidade da corrente que percorre o circuito.

c) Calcule a diferença de potencial entre os extremos de cada condutor.

d) Determine a potência dissipada por Efeito Joule no condutor de 1 Ω.

Resolução

Primeiro a que saber é, o que é uma associação de resistências em série. Para melhor entender é só imaginar como estão dispostos ou arrumados, vagões ou carruagens de um comboio (trêm). Verifica-se que no término de um vagão dá-se o início do outro, de uma forma sucessiva, assim também estão dispostos as resistências numa associação em série, onde as resistências estão todas conectadas pelo mesmo condutor sem desvio (nó).

a) Represente esquematicamente a associação e calcule a sua resistência equivalente.

Para fazer essa representação, deve-se entender bem o enunciado, com relação a disposição das resistências. Já está clarificado no parágrafo acima, mas vamos clarificar melhor a diferença de potencial (ddp), o enunciado diz que a ddp nos terminais da associação é 60 V, isso quer dizer que a tensão total da associação é 60 V, dessa forma o esquema fica:

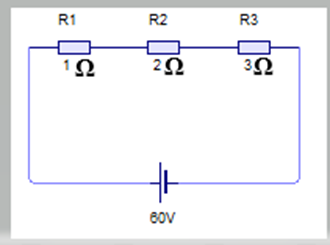
Cálculo da Resistência equivalente

R_eq = R₁ + R₂ + R₃

R_eq = 1 Ω + 2 Ω + 3 Ω

R_eq = 6 Ω

b) Determine a intensidade da corrente que percorre o circuito.

A intensidade da corrente que percorre o circuito, em outras palavras é a corrente total (I_T) que pede-se para calcular. Vamos então calcular essa grandeza com ajuda dos seguintes dados já conhecidos, U_T = 60 V e R_T = 6 Ω.

Tome nota que na associação em série a corrente que percorre no circuito em igual em todas as resistências, usando a equação de Ohm, temos:

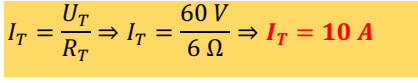
c) Calcule a diferença de potencial entre os extremos de cada condutor.

Numa associação em série a queda de tensão em cada resistência, o seu somatório é sempre igual a tensão da fonte, ou seja, como temos três resistências, então a tensão total de 60 V, vai se dividir em cada resistência, dessa forma fica:

Tensão na Resistência 1

U₁ = R₁ ∙ I₁

U₁ = 1 Ω ∙ 10 A

U₁ = 10 V

Tensão na Resistência 2

U₂ = R₂ ∙ I₂

U₂ = 2 Ω ∙ 10 A

U₂ = 20 V

Tensão na Resistência 3

U₃ = R₃ ∙ I₃

U₃ = 3 Ω ∙ 10 A

U₃ = 30 V

Olha que somando cada tensão (10 V + 20 V + 30 V = 60 V), exactamente o valor da fonte, então é sempre bom fazer essa verificação. E caso o somatório das quedas não coincidir com o valor da fonte, então os seus cálculos estão errados… REFAÇA!

d) Determine a potência dissipada por Efeito Joule no condutor de 1 Ω.

O condutor de 1 Ω é a resistência 1, então apenas vamos calcular a potência na R₁. Existem muitas formas de calcular a potência, vou resolver de duas formas diferentes:

Primeira forma:

P = R ∙ I²

P = 1 Ω ∙ (10 A)²

P = 100 W

Segunda forma:

Na resistência 1, a queda de tensão U₁ = 10 V e a corrente é I₁ = 10 A, dessa forma temos:

P = U ∙ I

P = 10 V ∙ 10 A

P = 100 W

35. Estão associados em série três condutores cujas resistências valem 5 Ω, 12 Ω e 15 Ω. A diferença de potencial entre os extremos da primeira resistência é 12 V. Calcule:

a) A intensidade da corrente eléctrica que passa pela associação.

b) A diferença de potencial entre os extremos dos condutores de 12 Ω e 15 Ω, respectivamente.

c) A diferença de potencial entre os extremos da associação.

d) A quantidade de energia que, por minuto, cada condutor transforma em calor.

Resolução

As três resistências estão associadas em série, sendo que a primeira R₁ = 5 Ω, tem nos seus terminais 12 V, isso quer dizer que a sua queda de tensão na primeira resistência  é U₁ = 12 V. Outros dados da associação são R₂ = 12 e R₃ = 15.

a) A intensidade da corrente eléctrica que passa pela associação.

Sabe-se que a associação é em série, e numa associação em série, a corrente que circula numa resistência é igual em todas as resistências, consequentemente também é igual a corrente total, ou seja, numa associação em série a corrente é a mesma em todo o circuito.

Então vejamos, já é conhecida o valor da tensão na primeira resistência U₁ = 12 V, assim também como é conhecida o valor da primeira resistência R₁ = 5 Ω, a partir desses valores pode-se calcular o valor da corrente eléctrica nessa resistência e consequentemente de todo o circuito, dessa forma temos:

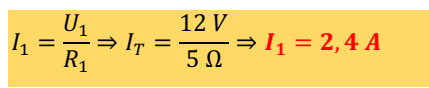
I₁ = I₂ = I₃ = I_T = 2,4 A

b) A diferença de potencial entre os extremos dos condutores de 12 Ω e 15 Ω, respectivamente.

O condutor de 12 Ω é segunda resistência, ou seja, R₂ = 12 Ω.

Enquanto o condutor de 15 Ω é a terceira resistência, isto é, R₃ = 15 Ω.

Para o cálculo das tensões, o valor da corrente a usar será de 2,4 A por ser igual em todo o circuito, dessa forma temos:

Tensão na Resistência 2

U₂ = R₂ ∙ I₂

U₂ = 12 Ω ∙ 2,4 A

U₂ = 28,8 V

Tensão na Resistência 3

U₃ = R₃ ∙ I₃

U₃ = 15 Ω ∙ 2,4 A

U₃ = 36 V

c) A diferença de potencial entre os extremos da associação.

A diferença de potencial entre os extremos, ou simplesmente, a tensão total do circuito, pode-se determinar de duas formas:

Primeira forma:

A soma algébrica de cada queda de tensão em cada resistência, corresponde a tensão total, dessa forma temos:

U_T = U₁ + U₂ + U₃

U_T = 12 V + 28,8 V + 36 V

U_T = 76,8 V

Segunda forma:

Uma vez sabido que a corrente que circula o circuito é 2,4 A, e a Resistência total é dada por:

R_T = R₁ + R₂ + R₃

R_T = 5 Ω + 12 Ω + 15 Ω

R_T = 32 Ω

Então aplicando a Lei de Ohm, temos:

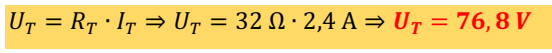
d) A quantidade de energia que, por minuto, cada condutor transforma em calor.

Falar de energia, calor, estamos em outra palavra falando de trabalho que é realizado num dado intervalo de tempo, nesse caso o tempo é 1 minuto que corresponde a 60 segundos.

Conhecido o valor da corrente e da tensão em cada resistência, então pode-se calcular a quantidade de energia transformada em calor por cada resistência, dessa forma fica:

Energia na Resistência 1

E₁ = U₁ ∙ I₁ ∙ t

E₁ = 12 V ∙ 2,4 A ∙ 60 s

E₁ = 1728 J

Energia na Resistência 2

E₂ = U₂ ∙ I₂ ∙ t

E₂ = 28,8 V ∙ 2,4 A ∙ 60 s

E₂ = 4147,2 J

Energia na Resistência 3

E₃ = U₃ ∙ I₃ ∙ t

E₃ = 36 V ∙ 2,4 A ∙ 60 s

E₃ = 5184 J

36. Estão associadas em série três resistências uma de 2 kΩ, outra de 0,5 kΩ e outra desconhecida. A diferença de potencial entre os extremos da associação é de 3 kV. Quanto deve valer à terceira resistência para qua a corrente seja de 0,75 A?

Resolução

Para a resolução desse exercício, primeiro vamos calcular o valor da resistência total, a partir da Lei de Ohm, sendo os valores da tensão e corrente total são respectivamente 3 kV e 0,75 A. De referir que a letra (k) associada a uma unidade vale mil, isso quer dizer, 3 kV = 3 ∙ 1000 V = 3000 V.

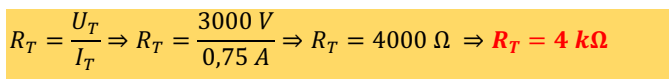
A partir desse valor, podemos encontrar a terceira resistência desconhecida, recorrendo a equação do cálculo da resistência total numa associação em serie, dessa forma temos:

R_T = R₁ + R₂ + R₃

4 kΩ = 2 kΩ + 0,5 kΩ + R₃

4 kΩ = 2,5 kΩ + R₃

R₃ = 4 kΩ – 2,5 kΩ

R₃ = 1,5 kΩ

R: O valor da terceira resistência desconhecida é 1,5 kΩ.

37. As dez lâmpadas de uma árvore de Natal estão ligadas em série. Numerando estas lâmpadas de 1 a 10 e supondo que a nona lâmpada queime:

a) As outras nove lâmpadas apagam.

b) Ficam acesas apenas as lâmpadas de 1 a 8.

c) Somente a nona lâmpada apaga.

d) Fica acesa somente a décima lâmpada.

Resolução

Uma forma simples de imaginar esse cenário, é o exemplo de como os vagões de comboio estão dispostos, se por acaso um dos vagões descarrilar (cair ou sair fora da linha), todos os vagões restantes ficam comprometidos, ou seja, o comboio pára, não anda.

Assim também acontece numa associação em série, se uma lâmpada funde, as restantes apagam, pois o circuito fica aberto.

Alínea a).