Movimento Rectilíneo Uniformemente Variado (M.R.U.V)
Movimento Variado
Maior parte dos eventos que ocorrem no nosso dia-a-dia, não são constantes, ou seja, eles são variados, por exemplo quando andamos ou corremos, geralmente começamos a correr com uma velocidade maior e ao longo do tempo vamos reduzindo na nossa velocidade, um outro exemplo claro são os carros, eles partem de um destino com uma certa velocidade, mais ao longo do trajecto a sua velocidade vai variando, aumentando ou reduzindo, então essa variação é o que define o movimento variado.
Ao contrário do Movimento Uniforme em que a velocidade era a mesma, ou seja, é constante, no Movimento Variado a velocidade é que varia, sendo essa característica o grande diferencial entre os dois tipos de movimento.
Leia Sobre: Movimento Rectilíneo Uniforme (MRU)
Uma vez que a velocidade vai variando, acaba originando uma nova grandeza chamada de aceleração, na verdade aceleração é a taxa da variação da velocidade por unidade de tempo, matematicamente é expressa por:

Movimento Rectilíneo Uniformemente Variado (M.R.U.V)
Movimento Rectilíneo Uniformemente Variado (M.R.U.V), é aquele movimento que ocorre numa linha recta, mas com uma velocidade variada, onde essa velocidade pode diminuir ou aumentar, então o aumento ou a diminuição da velocidade, divide o MRUV em dois, Movimento Rectilíneo Uniformemente Acelerado (MRUA) e Movimento Rectilíneo Uniformemente Retardado (MRUR), respectivamente.
Movimento Rectilíneo Uniformemente Acelerado (MRUA)
Movimento Rectilíneo Uniformemente Acelerado (MRUA) – é aquele que a velocidade aumenta em cada unidade de tempo, assim sendo a aceleração é positiva.
Equações e Gráficos do MRUA
Gráfico da Velocidade
Uma vez que a velocidade, vai aumentando em cada unidade de tempo, então o seu gráfico é uma linha recta oblíqua crescente.

Equação da velocidade no MRUA
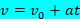
Onde:
v – velocidade final em m/s
v0 – velocidade inicial em m/s
a – aceleração em m/s2
t – tempo em s
Gráfico da aceleração
A aceleração no MRUA é uma linha recta horizontal, ou seja, tem um valor constante positivo.

Equação da aceleração

Onde:
∆ʋ – variação da velocidade em m/s
∆t – variação de tempo em s
Equação do espaço do MRUA

Onde:
S – espaço final em m
S0 – espaço inicial em m
Movimento Rectilíneo Uniformemente Retardado (MRUR)
Movimento Rectilíneo Uniformemente Retardado (MRUR) – é aquele que a velocidade diminui em cada unidade de tempo, assim sendo a aceleração é negativa.
Equações e Gráficos do MRUR
Gráfico da Velocidade
Uma vez que a velocidade, vai diminuído em cada unidade de tempo, então o seu gráfico é uma linha recta oblíqua decrescente.
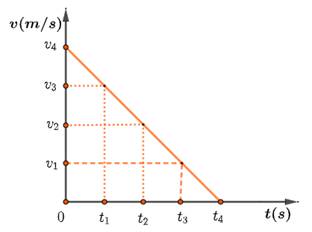
Equação da velocidade no MRUR

Onde:
v – velocidade final em m/s
v0 – velocidade inicial em m/s
a – aceleração em m/s2
t – tempo em s
Gráfico da aceleração
A aceleração no MRUR é uma linha recta horizontal, ou seja, tem um valor constante negativo.

Equação da aceleração

Onde:
a – aceleração em m/s2
∆ʋ – variação da velocidade em m/s
∆t – variação de tempo em s
Equação do espaço do MRUR

Onde:
S – espaço final em m
S0 – espaço inicial em m
Leis do MRUV
Lei da velocidade
A velocidade varia em proporções iguais, em intervalos de tempo iguais.

Lei da aceleração
A aceleração não muda, ou seja, é sempre a mesma – constante.

Exemplos
1. O movimento de um móvel animando de movimento uniforme é descrito pela seguinte tabela.
| v(m/s) | 4 | 8 | 12 | 16 | 20 |
| t(s) | 0 | 1 | 2 | 3 | 4 |
a) Classifique o movimento. Justifica.
b) Calcule a aceleração do móvel.
c) Qual é o espaço percorrido no final de 20 s.
d) Construa o gráfico de velocidade e aceleração.
Resolução
a) Classifique o movimento. Justifica.
R: Movimento Rectilíneo Uniformemente Acelerado (MRUA). Pois a velocidade aumenta em cada unidade de tempo.
b) Calcule a aceleração do móvel.






Comentários da Resolução
(1) e (2): Primeiro, antes de mais nada, escreveu-se a equação para o cálculo da aceleração.
(3): Fez-se as substituições dos respectivos valores na fórmula, incluindo as suas unidades. De notar que no ponto 3, a unidade m/s, o segundo está a dividir então podemos passá-lo para o denominador.
(4) e (5): Uma vez todos os dados inseridos, faz-se a manipulação matemática, ou seja, operações matemáticas básicas, incluindo as suas unidades, uma vez tendo baixado para o denominador a unidade s, acontece que no denominador já tem lá também a unidade s, ficando então (s x s). Olhando atentamente o ponto 5, fez-se a divisão de 16/4, e a multiplicação de (s x s), resultando em s2 no denominador, resultando assim na unidade da aceleração m/s2.
c) Qual é o espaço percorrido no final de 20 s.







Comentários da Resolução
(1) e (2): Primeiro, antes de mais nada, escreveu-se a equação para o cálculo da aceleração. Fez-se as substituições dos respectivos valores na fórmula, incluindo as suas unidades. De notar que o espaço inicial S0 = 0 m, isso deve-se por causa de no exercício não ser informado o valor do espaço inicial, assim sendo considera-se 0.
(3): Fez a simplificação das unidades, resultando em única unidade, o metro (m), olha que o tempo na fórmula está ao quadrado, assim sendo a sua unidade também será o quadrado, ou seja, será s2.
(4); (5) e (6): A este ponto, não nos resta mais nada a não ser simplesmente fazermos esses cálculos básicos, e no final darmos o resultado final, em função da sua unidade de medida.
d) Construa o gráfico de velocidade e aceleração.
Gráfico da aceleração
Uma vez a calculada a aceleração na alínea a) que foi 4 m/s2, então isso quer dizer que essa aceleração será constante durante todo o movimento, então o seu gráfico, é dado abaixo:

Gráfico da velocidade
Para a construção do gráfico da velocidade, recorre-se a tabela do enunciado, onde será feita uma correspondência entre os valores da velocidade nos seus respectivos tempos.
| v(m/s) | 4 | 8 | 12 | 16 | 20 |
| t(s) | 0 | 1 | 2 | 3 | 4 |


